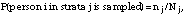
Respondents were randomly sampled within strata. For a predetermined number of respondents to be drawn from strata j, nj,
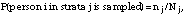
where Nj is the total number of persons in strata j in the sampling frame. In the absence of nonresponse and ineligibility issues, the weight for person i in strata j would simply be Wi = Nj/nj However, nonresponse and ineligibility affect nj and Nj, respectively, and they must be adjusted to arrive at weights that will allow proper inference back to the population of interest.
Nonresponse[1] was accounted for using the propensity score method of Little and Rubin (1987) to determine the probability that person i responds given that person i was sampled. This probability was calculated by fitting the logistic regression model
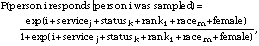
where i is the intercept coefficient and the other coefficients are the coefficients for indicator variables corresponding to person i's membership in various groups:
From this, the probability that person i in strata j was sampled and responded, pr(i), was calculated as
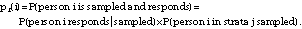
Similar to the propensity score model for nonresponse, strata sizes were adjusted for ineligibility using a logistic regression model. A model was fit that expressed the probability that a person listed in the Gulf War database was not in ODS/DS based on demographic characteristics. The model was fit to all survey respondents (the eligibles) versus those in the sampling frame who were reached but indicated that they had not served in ODS/DS (the ineligibles). The model is thus similar to the nonresponse model, although the covariates differed to reflect the dimensions important to ineligibility:

where, as before, i is the intercept coefficient and the other coefficients are the coefficients for indicator variables corresponding to person i's membership in the previously described groups (less status) plus:
To estimate the correct size of the strata, these probabilities were calculated for each of the 536,790 people in the Gulf War database and summed by strata. Thus
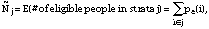
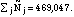 Using the adjusted strata sizes, the final analytic weights for each respondent
were calculated as
Using the adjusted strata sizes, the final analytic weights for each respondent
were calculated as
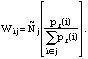
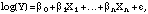
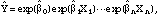
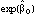 can be interpreted as the average pesticide use for the baseline group, and
can be interpreted as the average pesticide use for the baseline group, and
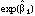 can be expressed as the percentage change from the baseline rate for a member
of the ith demographic group. The baseline group is defined as the group
corresponding to having all the indicator Xs in the model set to zero.
can be expressed as the percentage change from the baseline rate for a member
of the ith demographic group. The baseline group is defined as the group
corresponding to having all the indicator Xs in the model set to zero.Tables 4.7 and 4.8 are based on standard logistic regression models, using the whole respondent population, with a dependent variable that simply indicates whether each respondent said he or she used a particular pesticide form or not. In logistic regression, the log-odds is assumed to be a linear function of various covariates. Thus, the basic form of the model is
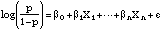
This means that the odds, p/(1 - p), can be expressed as a multiplicative
function of the fitted coefficients. Since the covariates in the model are all
indicator functions for respondent membership in various demographic
categories, the exponentiated coefficients can be expressed as the percentage
change in the estimated baseline group's odds,
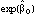 .
.
The logistic regression results for PB pill usage presented in Chapter Five are based on a similar model--the dependent variable is whether a respondent took PB pills or not--with the same set of covariates.
Standard errors in both the linear and logistic regression models were adjusted for stratified sampling as discussed in the previous subsection.
When the active ingredient could not be uniquely determined from the information given, all possibilities were recorded. For example, a spray that smelled like insecticide that was used on the uniform could have had either permethrin or DEET as the active ingredient. In such a case, both possibilities were allowed. Then later, as discussed in the next section, the probabilities of whether the spray was permethrin or DEET were imputed from the distribution of uniquely identified active ingredients.
For unnamed products, it was assumed that the pesticide was appropriately used when classifying it. For example, sprays that were used on the body only are assumed to be DEET-based and not permethrin (which should have been used on uniforms).
If a pesticide name from the survey list was given, then the active ingredient was classified according to the "rules" listed in Table C.1.
| Product Name | Active Ingredient |
| DEET, Insect/Arthropod Repellent, Cutter Insect Repellent, Off, 3M Repellent, any Cutter personal products, 3M, Repellent | DEET |
| Permenone; any combination and/or permutation of the following words: Wasp Freeze, Hornet Killer, Wasp Stopper, Raid | Permethrin |
| Diazinon Dust, Diazinon 4E; Diazol | Diazinon |
| 6-12 | Ethyl hexanediol |
| DDT | DDT |
| Parathion | Parathion |
| Chigg-Away | Sulfur |
| Skin-So-Soft | none |
If an "other" name was provided, that name was first used to try to identify the active ingredient. Rules for this are listed in Table C.2.
| If the "Other" Response Contained: | Active Ingredient |
| DEET, Deep Woods, Off, Bug Juice, Bug Dope, Muskol | DEET |
| Permenal, perminal, permithen, permithium, peramone, permenone | Permethrin |
| 6-12, 6-22 | Ethyl hexanediol |
| Phenitrin, d�phen | d-Phenothrin |
| DDT | DDT |
| Parathion | Parathion |
| Gig-away | Sulfur |
| Hawaiian Tropic, Skintastic,a Soft Scent, Lubriderm | None |
aSkintastic, a product with pesticide ingredients, was not available in 1990-1991. We thus assumed that it was a nonpesticide commercial lotion.
For unnamed pesticides and those pesticides that could not be classified according to the "other" name given, the active ingredient was inferred from some combination of form, color, smell, and use. The rules for this classification are given in Table C.3.
| Form | Color | Smell | Use | Active Ingredient |
| Spray | n/a | Off, DEET, or sweet | Any | DEET |
| Spray | n/a | Raid | Any | Permethrin |
| Spray | n/a | Insecticide or chemical | Body | DEET |
| Spray | n/a | Insecticide or chemical | Uniform or body and uniform | DEET or permethrin |
| Powder | White, cloudy, cream, yellow, or gray | Insecticide, chemical, or musty | Any | Lindane |
| Liquid | Clear | Sweet, off | Any | DEET |
| Liquid | White, clear, light brown, or yellow | Sulfur | Any | Sulfur |
| Liquid | White or yellow | Insecticide or chemical | Any | Permethrin |
| Liquid | Clear | Insecticide or chemical | Body | DEET |
| Liquid | Clear | Insecticide or chemical | Uniform or body and uniform | DEET or permethrin |
| Lotion | White, clear, light brown, or yellow | Sulfur | Any | Sulfur |
| Lotion | White, cloudy, cream, or clear | Insecticide or chemical | Any | DEET |
| Stick or Wipe | Any | Any | Any | DEET, Ethyl hexanediol |
If the active ingredient could not be classified via the rules in Tables C.2 and C.3, but a physical description of a military-issue container was provided, the rules in Table C.4 were used.
| If the "Other" Response Indicated The Pesticide Was Military Issue And It Met The Following Conditions: | |||
| Form | Use | Other Conditions | Active Ingredient |
| Liquid or spray | Body | DEET | |
| Liquid or spray | Uniform or body and uniform | DEET or Permethrin | |
| Liquid | Any | Comments or smell field gave a sulfur smell | Sulfur |
| Lotion | Any | Comments indicated a "tube" container | DEET |
| Lotion | Any | Comments indicated a "bottle" or "green" container | DEET |
| Powder | Any | Comments or smell field gave a musty smell | Lindane |
Finally, if only a subset of the information was given, say form and color but not smell, then the response was mapped to all possibilities with matching form and color. If color or smell did not map to those values in the table, it was treated as missing. In the most extreme case, if both smell and color were missing, then the response was mapped to all the active ingredients for that form (consistent with the reported use).
Probability of Active Ingredient Estimation. To estimate the probability that a respondent used an active ingredient, we used a methodology motivated by the EM algorithm of Dempster, Laird, and Rubin (1977). Since the distribution of pesticides varied by demographic characteristics, personnel were grouped into similar cohorts to condition the calculations on those characteristics. Sprays and liquids were conditioned on service and usage (body, uniform, or body and uniform); all others were conditioned on service and gender.[3]
Let pd, pp, pb, and po be the unknown probability that a random individual in the cohort used the active ingredients DEET, permethrin, sulfur, and "other," respectively. For a given respondent in the cohort, let Id, Ip, Ib, and Io be indicators derived from the classification scheme for whether the respondent may have used each of the active ingredients.
For each cohort, the distribution of pesticide use was imputed as follows. First, all the uniquely identifiable pesticides were used to generate an initial estimate of the distribution on active ingredients. For a given cohort, this was estimated as
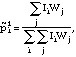
for all j in the cohort and where i = d, p, b, or o. Then, each individual's probability of using an active ingredient was estimated as
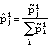
The cohort's overall probabilities and individual probabilities are then iteratively reestimated by alternating between
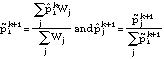
until
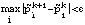
We ultimately used
 = 0.01 after empirically determining that the final result was insensitive to
further reductions in
= 0.01 after empirically determining that the final result was insensitive to
further reductions in
 .
.
Estimation of Frequency of Use. To estimate the frequency of use for each active ingredient by the fraction of the population represented by person i, it was necessary to combine the various frequencies of use between and within forms. For example, person i may have used two sprays and one liquid, each of which had some probability of being DEET and another probability of being permethrin, and each had a reported frequency of usage. Some individuals in Wi, the fraction of ODS/DS population represented by person i, may have used all DEET products, so that their DEET usage is the sum of the three use frequencies and their permethrin usage is zero. Others may have used all permethrin products and no DEET, and still others may have used some combination of active ingredients.
To estimate the fraction of each Wi that used a particular active ingredient with a particular frequency, we assumed that for each person the probability of using one product was independent of the probability of using another product. Each person could have reported using up to nine personal products (three sprays, three liquids, and three lotions) that could have contained the active ingredients of interest (DEET, permethrin, and sulfur). Each product reported had a frequency of use and an imputed probability distribution on the three possible active ingredients and "other nonpesticide."[4] For each person, let fij be the reported frequency of use for product j, j = 1, . . . 9. Let pijk be the imputed probability that product j has active ingredient k. Finally, let Ij be an indicator variable for product j and let the group of nine indicators I form a column vector. There are 2(9-1) = 511 possible vectors for which at least one indicator is nonzero. Each vector represents a combination of products that might have contained a particular active ingredient.
Then, for each indicator vector, we calculated
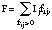
and for each F > 0 we then calculated
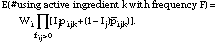
The result is that each survey respondent's weight, Wi, is apportioned by active ingredient and frequency of use within active ingredient.
Estimation of Standard Errors. To capture the uncertainty resulting
from the imputation of active ingredients, we used the Bootstrap (Efron and
Tibshirani, 1993) to calculate standard errors. For a given statistic, say the
mean frequency of usage of an active ingredient, its standard error is
calculated as follows. Let
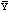 be the mean frequency of usage calculated. Then the Bootstrap proceeds to
resample with replacement from the original observations. Because this was a
stratified random sample, the resampling was done with replacement within
strata, maintaining the total number of resampled observations within each
stratum equal to the original number of respondents in each stratum. After
each resample was drawn, the entire imputation was redone, and a new bootstrap
statistic,
be the mean frequency of usage calculated. Then the Bootstrap proceeds to
resample with replacement from the original observations. Because this was a
stratified random sample, the resampling was done with replacement within
strata, maintaining the total number of resampled observations within each
stratum equal to the original number of respondents in each stratum. After
each resample was drawn, the entire imputation was redone, and a new bootstrap
statistic,
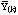 ,
was calculated, k = 1, . . . ,M. From these bootstrap statistics
,
was calculated, k = 1, . . . ,M. From these bootstrap statistics
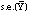 is
estimated as
is
estimated as
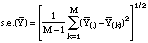
where
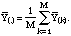
We ultimately used M = 200 in the calculations, consistent with what is normally recommended (Efron and Tibshirani, 1993), as our results differed insignificantly for M = 400.
[1]"Nonresponse" as used in this appendix includes those who refused to participate and those who were not located--essentially everyone in the sampling frame who did not complete the survey, minus those who were ineligible.
[2]Except for the imputation of personal-use active ingredients in Tables 3.10 to 3.12, as described in the next section.
[3]Additional conditioning was not possible of because small cell sizes.
[4]Although the survey asked only about pesticides, respondents sometimes reported nonpesticides. Thus, to avoid bias in the imputation, we also imputed from the nonpesticides and estimated a probability that a product was not a pesticide.